Следующая загадка возникает тогда, когда мы изучаем субатомные “частицы”, известные как кварки. Когда атомная структура вдруг разрушается, в пузырьковой камере появляются короткие траектории, которые будут отлетать от нормального спиралевидного пути “частицы”; они и были названы “кварками”. После высвобождения, “кварки” очень быстро исчезают. Геометрия их движений была тщательно проанализирована, поскольку единственное, что вы можете по-настоящему определить при анализе посредством пузырьковой камеры, это разные геометрические формы движения. Было открыто много разных форм “кварков”, причем каждая форма обладала разными геометрическими свойствами, ошибочно называемыми “цветом”, “шармом” и “странностью”. Мюррей Гелл-Манн первым создал единую модель, демонстрирующую как именно взаимосвязаны эти разные геометрические свойства. Он назвал ее “Восьмеричным Путем”. Замечательно, что единая геометрическая структура, которую мы видим, - тетраэдр:

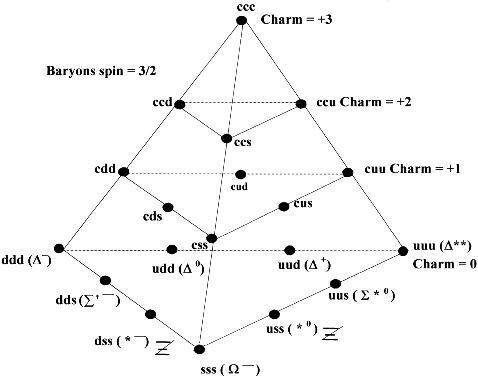
Рис. 4.9 Тетраэдр, видимый в организации “кварков”  “Восьмеричного Пути” Гелл-Манна

Итак, что же мы видим? Очевидно, что каждая точка – это отдельный “кварк”. Джонсон утверждает, что “кварки” высвобождаются тогда, когда эфирный энергетический поток тетраэдра внутри атома вдруг разрушается. В течение короткого промежутка времени, высвобожденные энергетические фрагменты будут продолжать течь с теми же свойствами вращения/геометрии, которыми они обладали, будучи связанны в атоме; но они очень быстро возвращаются обратно в эфир. Разные “кварки” не следует рассматривать как возникшие в результате разрушения одного атома, поскольку угол, под которым разрушается атом, определяет, какая часть его внутреннего геометрического Единства будет высвобождена. Поэтому кварки следует тщательно изучать по отдельности. А вот что еще интереснее: в модели Гелл-Манна находятся и другие “свернутые” геометрические частоты, такие как куб-октаэдр; просто тетраэдр – это одна из трех разных открытых им иерархий.

И вновь, традиционный научный мир рассматривает Восьмеричный Путь Гелл-Манна как просто удобную геометрическую организацию, и ничего больше. В следующем отрывке д-р Мило Вольф указывает на тот факт, что геометрия могла бы быть решением для понимания структуры “ядерных пространственных резонансов” в квантовой сфере (страница 198 его книги):

“Другая интересная проблема с полезным результатом – увидеть, можно ли обнаружить способ связать ядерные пространственные резонансы с объяснением теории групп зоопарка ядерных частиц. Одно из названий этой теории – Восьмеричный Путь, открытый Гелл-Манном и Нееманом в 1960 году. Теория умно использует геометрическое группирование для определения их параметров: спина, четности, числа изотопов, числа странностей. Теория групп еще не раскрыла физическую структуру, такую как пространственные резонансы. Если связь существует, тогда логично ожидать, что решения уравнения волны пространственного резонанса обладали бы ортогональными свойствами, соответствующими Восьмеричному Пути. Волнующая перспектива”.

Интересно: когда мы заканчивали эту часть книги, с нами связался д-р Р. Б. Дункан, опубликовавший в Интернете очень детальную и основательную работу, объясняющую структуру атома с точки зрения теории групп, упомянутой выше Вольфом. Прежде, чем опубликовать решение, Дункан работал над этой проблемой тридцать лет!